Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js
Mathematisms

An Application of Burnside's Lemma to Computer Science

1. Introduction

A couple years ago - back when I still coded things - I stumbled across a seemingly-innocent problem in computer science about permuting matrices of numbers. Initially, I thought the problem just needed a little algorithmic speedup in order to work; however, the deeper I dived, the more I realized how mathematical the structure behind this problem was.

In the end, my solution was actually primarily mathematical, drawing from group-theoretic ideas to optimize the algorithm. This problem means quite a lot to me, because it was one of the first times I actually applied higher mathematics to a non-mathematical problem, and I think it’s one of the reasons why I love math as much as I do today.

The problem is as follows: Let M be the set of all w×h matrices whose elements are drawn from the set {1,…,n}, and let S be a subset of M such that no element of S can be rearranged into another one by permuting its rows and columns. Given w,h, and n, compute the largest possible size of S.

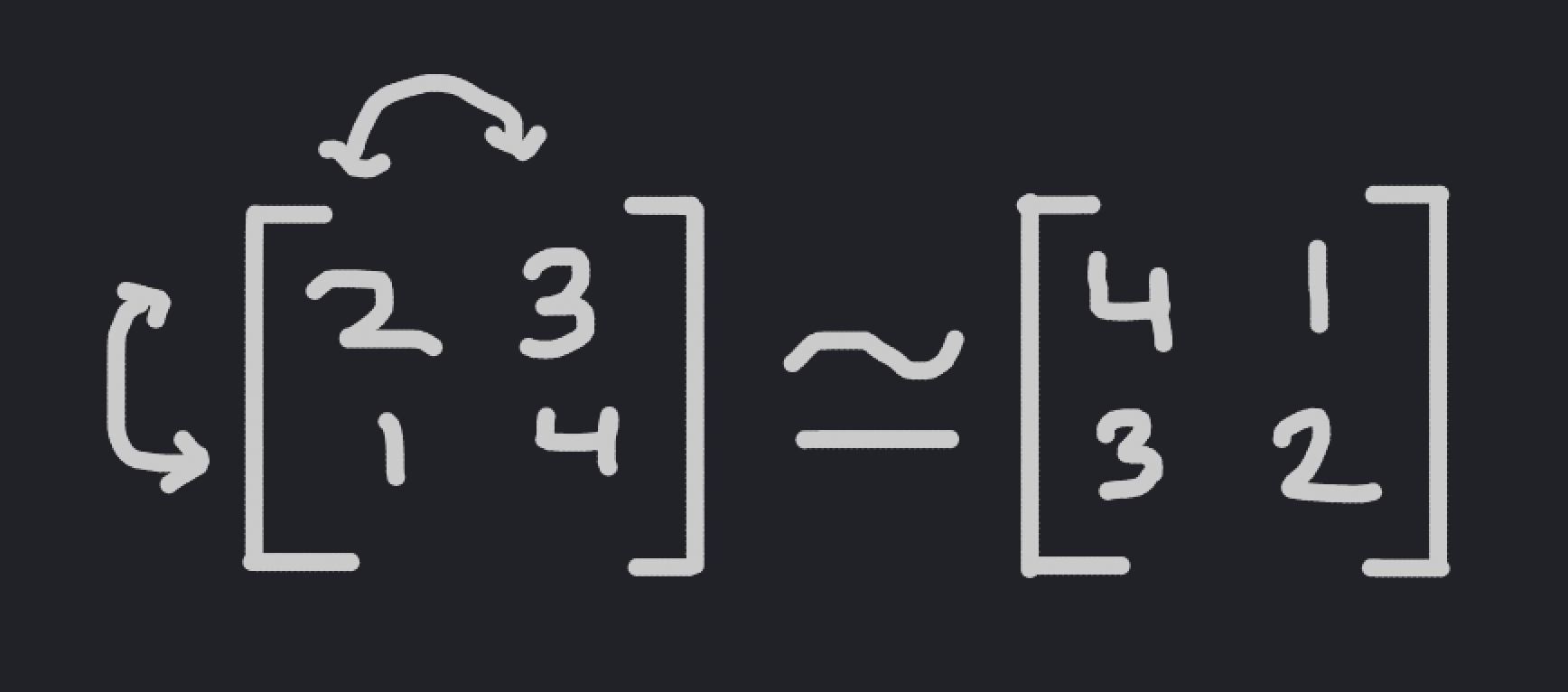
Permutation Example

An example of two matrices that can be...

read more

An Intuitive Explanation of Monsky's Theorem

1. Introduction

Let’s set the scene. I (16M) am a huge fan of Minecraft. As such, since my birthday is coming up, I obviously want to get a Minecraft themed birthday party - this will include a pig pinata, Minecraft themed utensils, and obviously, a Minecraft cake.

Minecraft Cake

A wonderful Minecraft cake.

When it comes time to cut the cake, I’ve only got a couple of - relatively self explanatory - rules. Obviously, I want every cut of the cake to be a triangle (for the sake of tradition), and I want every single cut to have an equal area, to avoid situations like this.

Slightly Less Cake

He got slightly less cake.

I invited six people other than me to my birthday party. How should I cut the cake?

At a first glance, it seems like there has to be a solution. I mean, there’s an infinite variety of ways to cut a cake into 7 triangles - surely one of them is such that all the triangles have equal area, right?

In fact, I encourage you to give this problem a shot! Try to split a...

read more